QuarkXPress How-To: Working with the Bézier and Freehand Tools

Creativepro.com readers can subscribe to Element K Journals at a discount. Click here to learn more.
Although QuarkXPress isn’t technically a drawing program, the engineering of Bézier and Freehand tools in version 4 certainly opened a world of opportunity and creativity for many users. As shown in Figure A, it’s possible to produce graphics beyond that of ordinary geometric shapes using a combination of just these tools in QuarkXPress. As with all tools, though, you probably won’t be able to just select one and create a masterpiece. They require a little practice, patience and understanding. But before you know it, they’ll enable you to create professionally drawn Bézier items and, consequently, design better-looking pages than ever before.
 Figure A: The Bézier and Freehand tools in QuarkXPress enable you to create graphics beyond ordinary geometric shapes.
Figure A: The Bézier and Freehand tools in QuarkXPress enable you to create graphics beyond ordinary geometric shapes.
Where to Begin?
We can’t provide you with patience, but stick with us and you’ll get the practice and understanding you need to use the Bézier and Freehand tools in QuarkXPress. In this article, we’ll start with a little history on the origin of the term Bézier. Then we’ll introduce you to the various Bézier and Freehand tools in QuarkXPress so you become more familiar with them and understand their underlying principles. Lastly, we’ll show you how to control and ma-nipulate the tools and the paths they create. Upon this article’s completion, you should have a reasonable level of understanding of these handy tools.
What Exactly is a Bézier?
The term Bézier (BAY-z-aye) stems from the name of mathematician Pierre Bézier, who formulated principles upon which vector objects are based. In simple terms, his theory states that all shapes are composed of segments and points. Segments may be either curved or straight while their condition and shape are controlled by properties of the points that join them. A collection of two or more points that form a straight or curved segment is referred to as a path. Two or more paths combined to form a broken or non-continuous series of segments and points are called a compound path. And that’s your math lesson for today.
The Right Tool for the Job
Bézier drawing supports Pierre’s theory with the inclusion of the four Bézier tools and four Freehand tools shown in Figure B. Both sets of tools create items based on line segments and points, but each has a slightly different purpose.
 Figure B: Each Bézier and Freehand tool has its own unique quality and function.
Figure B: Each Bézier and Freehand tool has its own unique quality and function.
For example, Freehand tools can be used to draw Bézier text boxes, picture boxes, lines and text paths of any shape. However, they’re kind of hard to draw with and, therefore, best left for drawing items that aren’t meant to be precise. Bézier tools can be used to create the same inventory of items but offer point-by-point control, which enables you to do more precise drawing. Bézier tools also enable you to create fewer points than a Freehand tool. This is advantageous because the more points on a path, the more difficult it is to edit, the more memory it consumes, and the more time it takes to print.
Anatomy of a Bézier Path
Before you grapple too hard with using these tools, it may help you to know a bit about the onscreen information provided by QuarkXPress that reflects the points and segments they create. As mentioned earlier, line segments are either straight or curved, as shown in Figure C. Straight segments are joined end to end with corner points, while curved segments are controlled by the properties of their adjoining smooth or symmetrical points.
 Figure C: Curved and/or straight segments are connected with points to create a path that forms a shape.
Figure C: Curved and/or straight segments are connected with points to create a path that forms a shape.
Every smooth and symmetrical point created with a Bézier or Freehand tool has two curve handles. One handle controls the shape of the preceding segment, while the other controls the shape of the segment to follow. The exception to this rule is the first and last points of an open path, known as endpoints, drawn with a Freehand line tool, which have only one curve han-dle to control their respective segments. The different characteristics of each type of point are as follows:
- Corner point.This type of point connects two straight lines, a straight line and a curved line or two non-continuous curved lines. Both segments on either side of a corner point can be manipulated independently. Corner points don’t have curve handles unless converted from a smooth or symmetrical point.
- Smooth point.
- As the name sug-gests, a smooth point creates a smooth transition between two curved segments, as shown in Figure D. Its curve handles can be sized individually to edit the shape of the segments it joins but always remain in alignment to keep the curved segment continuous.
 Figure D: Smooth points create continuous curved line segments.
Figure D: Smooth points create continuous curved line segments.
- Symmetrical point.
This type of point forces the curved segment on either side of it to be equal in slope and angle, as shown in Figure E. A symmetrical point’s curve handles are always aligned and an equal distance to each other so both segments remain symmetrical.
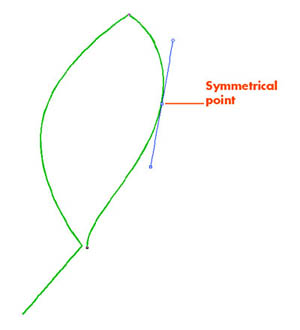
Figure E: Symmetrical points create equal, continuous curved segments.

